Learning Objectives
- Dependent and Independent Variables
- Equation of a Straight Line
- Linear Regression
Dependent and Independent Variables
- So far, you've been studying input and output/target variables. Commonly, the input variable is known as the independent variable, and the target variable is known as the dependent variable.
- In a nutshell, our target variable is nothing but a dependent variable. Why dependent? Because the values of this variable are dependent on other variables (i.e., input variables)
- And, our input variables are known as independent variables. Here the values of these variables are not dependent on any other variables.
Let's look at some examples to learn more about them!
- Look at the Standard Metropolitan Areas Data below. In the dataset, we might be curious to predict "crime_rate" in the future, so that becomes our target variable (dependent variable) and the rest of the variables become input variables (independent variables) for building a machine learning model.

Another Example
- A scientist wants to see if a light's brightness affects how much a moth is attracted to it.
- The scientist controls the brightness of the light. This would be the independent variable.
- The dependent variable would be how the moth reacts to the different light levels (distance to the light source).
Equation of a Straight Line
- In algebra, a linear equation (equation of a straight line) typically takes the form y = mx + b, where m and b are constants, x is the independent variable, and y is the dependent variable.
- Basically, the value of y is calculated using x, whereas x has no dependence on the value of y.
y = how far up
x = how far along
m = Slope or Gradient (how steep the line is)
b = value of y when x=0

- How do you find "m" and "b"?
- b is easy: just see where the line crosses the Y axis.
- m (the Slope) needs some calculation:

Synonyms Recap
Too many synonyms to memorize? Let me put them all down in one place for better understanding:
- Variables = Features
- Input Variables = Attributes = Predictor = Independent Variables
- Target Variables = Labels = Outcomes = Dependent Variables
Linear Regression
What is linear regression? - an example
Suppose you are thinking of selling your home. And various houses around you with different sizes (area in sq. ft) around you have sold for different prices as listed below:

And considering your home is 3000 square feet. How much should you sell it for?
Well! You have to look at the existing price patterns (data) and predict a price for your home. This is called linear regression.
Here's an easy way to do it. Plotting the 3 data points we have so far:

Each point represents one home.
Now you can eyeball it and roughly draw a line close to all of these points. Then look at the price shown by the line, where the square footage is 3000:
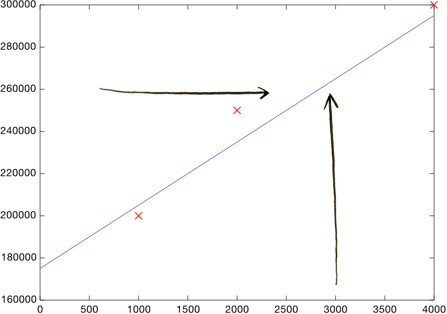
Boom! Your home should sell for $260,000.
That's all! You plot your data, make a rough line, and use the line to make predictions. You need to make sure your line fits the data well:

But of course, we don't want to make a line roughly; we want to compute the exact line that best "fits" our data. That's where machine learning comes into play!
What is linear regression?
- Linear regression is a linear model, i.e., a model that assumes a linear relationship (straight-line relationship) between the input variables (x) and the single output variable (y).
- When there is a single input variable (x), the method is called simple linear regression or just linear regression. E.g., the Salary dataset given here. There is only one target variable and one input variable where we are predicting the salary of individuals using their years of experience.
- When there are multiple input variables, it is often referred to as multiple linear regression. E.g., Smart Metropolitan areas data set, we have multiple input variables.
References
Slide Download Link
You can download the slides for this topic from here.