Learning Objectives

• Linear Algebra
• Matrices

What is Linear Algebra?

Often the first acquaintance with linear algebra looks something like this:

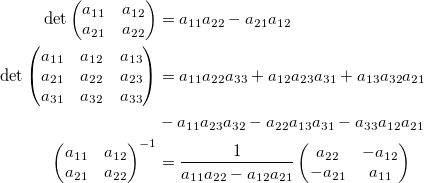
Not very inspiring, right? Two questions immediately arise: where did all this come from, and why is it needed?

Basic definition: Linear algebra is a sub-field of mathematics concerned with vectors, matrices, and linear transforms.

Do You Need Linear Algebra?

• It depends on your goal.
• If you want to use AI and machine learning tools as a black box, you arguably need just enough math to figure out if your problem fits the model's premise.
• But, Linear Algebra is a must-learn if you want to develop new ideas. I don't mean you need to learn everything concerning math. Doing so, you will be stuck at everything and lose motivation towards other more important things like calculus/stats.
• Mathematics in data science and machine learning is not about crunching numbers but about what is happening, why it's happening, and how we can play around with different things to obtain the desired results.

Linear Algebra

• Let's start with a simple problem.
  • Condition 1: Imagine the price of two chocolates and one apple is 100 units
  • Condition 2: Similarly, imagine the price of one chocolate and two apples is 100 units.
    Now, we want to find the price of 1 chocolate and an apple.
• Suppose the price of 1 chocolate is $x and the price of an apple is $y. Values of 'x' and 'y' can be anything depending on the situation, i.e., 'x' and 'y' are variables.
• Translating the above information in mathematical form:
         Equation (1)
         Equation (2)
• To find the prices of chocolate and apple, we need the values of 'x' and 'y' such that it satisfies both the equations.
• The fundamental problem of linear algebra is to find these values of 'x' and 'y' which is nothing but the solution to a set of linear equations.

Graphical Representation of two Equations

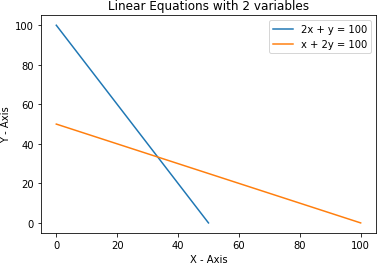
The intersection point is the solution to these two equations.

Complicating the Problem

• In the earlier example, we had two variables, 'x' representing the price of chocolate and 'y' representing the price of an apple.
• Now, suppose you are given a set of three conditions with three variables, say 'x', 'y', and 'z', and asked to find the value of three variables.
• The three conditions are given as:
         Equation (1)
           Equation (2)
             Equation (3)
• By solving the above three equations, we can get the values for 'x', 'y', and 'z'.
• In Linear Algebra, data is represented as linear equations. These linear equations are, in turn, described in the form of matrices and vectors.

Matrices

• A matrix is a form of representing data in the form of rows and columns. It is a very natural approach to organizing data.
• A real-life example:
  Consider a reactor that needs to be controlled using multiple attributes from various sensors like Pressure (P), Temperature (T), Density (d), etc.

In the matrix above:

• The first column represents Pressure (P)
• The second column represents Temperature (T)
• The third column represents Density (d)
• Each row corresponds to one sample.

Linear Equations in Matrix Form

• Earlier, we had two linear equations:
         Equation (1)
         Equation (2)
• The above two linear equations can be represented in the matrix form as:
  
  
• We can get the above two linear equations from the shown matrix equation by multiplying the two matrices on the left-hand side and equating the corresponding value to the right-hand side.
• Here is an excellent resource on Matrices for further reading: https://www.statisticshowto.com/matrices-and-matrix-algebra/

Additional Resources

• Interested to learn more about linear algebra operations in Machine Learning?
• Check out this helpful resource: https://machinelearningmastery.com/linear-algebra-cheat-sheet-for-machine-learning/

PS: Matrix operations like Addition, Multiplication, and Transposing are commonly used in ML.