Objetivos de aprendizaje

• Clasificación y función Sigmoidea
• Funciones de activación
• Métodos de construcción de modelos de Deep Learning
• Funciones de error y optimizadores

En la unidad anterior, aprendiste sobre el funcionamiento de un Neural Red a nivel conceptual.

En este módulo, comprenderá cómo todos esos conceptos se ponen en práctica al comprender algunos componentes cruciales de una red neuronal.

Finalmente, construirá un modelo para detectar si una persona tiene una enfermedad cardíaca o no.

Clasificación, importancia de la función sigmoidea y resumen de la regresión logística

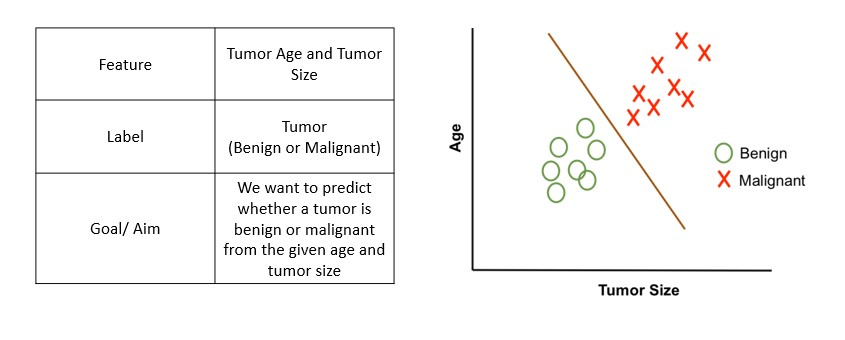
¿Qué es la Clasificación?

Aprendamos con algunos ejemplos:

• En clasificación, clasificamos el resultado en dos clases (Ej: sí o no)
• Ejemplos:
  • Predecir si una transacción es fraudulenta o no
  • Predecir si dar un préstamo o no
  • Predecir si otorgar admisión a la universidad o no
  • Nota: Puede haber problemas de clasificación con más de dos clases, y se llama clasificación múltiple

¿Qué es la clasificación múltiple?

Es tan simple como dividir los desechos en cuatro categorías: plástico, vidrio, metal y papel (hablaremos de la clasificación múltiple en unidades posteriores).

Regresión logística

• La regresión logística es uno de los algoritmos básicos y populares para resolver problemas de clasificación binaria
• Para cada entrada, la regresión logística genera una probabilidad de que esta entrada pertenezca a las dos clases
  • Establecer un límite de umbral de probabilidad que determine a qué clase pertenece la entrada
• Problemas de clasificación binaria (2 clases):
  • Correos electrónicos (Spam / No Spam)
  • Transacciones con Tarjeta de Crédito (Fraudulentas / No Fraudulentas)
  • Incumplimiento de préstamo (Sí / No)

Ahora, puede preguntar, ¿por qué no usamos la regresión lineal? Porque nosotros ¿Necesitas un nuevo algoritmo?

Bueno, encontrará todas las respuestas en el video en las siguientes diapositivas.

¡El video a continuación es imprescindible, ya que el instructor ha explicado brillantemente la regresión logística!

Regresión lineal vs. logística

• La regresión lineal se usa para resolver problemas de regresión con valores continuos
• La regresión logística se utiliza para resolver problemas de clasificación con categorías discretas
  • Clasificación binaria (Clases 0 y 1)
  • Ejemplos:
    • Correos electrónicos (Spam / No Spam)
    • Transacciones con Tarjeta de Crédito (Fraudulentas / No Fraudulentas)
    • Incumplimiento de préstamo (Sí / No)
• Supongamos que un científico de datos llamado John quiere predecir si un cliente comprará un seguro o no.
• Recuerde que la regresión lineal se usa para predecir un continuo valor donde la salida (y) puede variar entre (infinito positivo) a (infinito negativo), mientras que en este caso, la variable objetivo (y) toma solo dos valores discretos, 0 (sin seguro) y 1 (Sí, tengo el seguro).
• John decide ampliar los conceptos de regresión lineal para cumplir con su requisito. Un enfoque es tomar la salida de la regresión lineal y mapearla entre 0 y 1; si la producción resultante está por debajo de cierto umbral (por ejemplo, 0,5), clasifíquelo como No (no compró el seguro), mientras que si el resultado está por encima de cierto umbral, clasifíquelo como comprando el seguro (sí)
• Luego trazamos una línea de regresión lineal simple y establecemos el umbral en 0.5
  • Clase negativa (Seguro = No) – Edad en el lado izquierdo
  • Clase positiva (Seguro = Sí) – Edad en el lado derecho

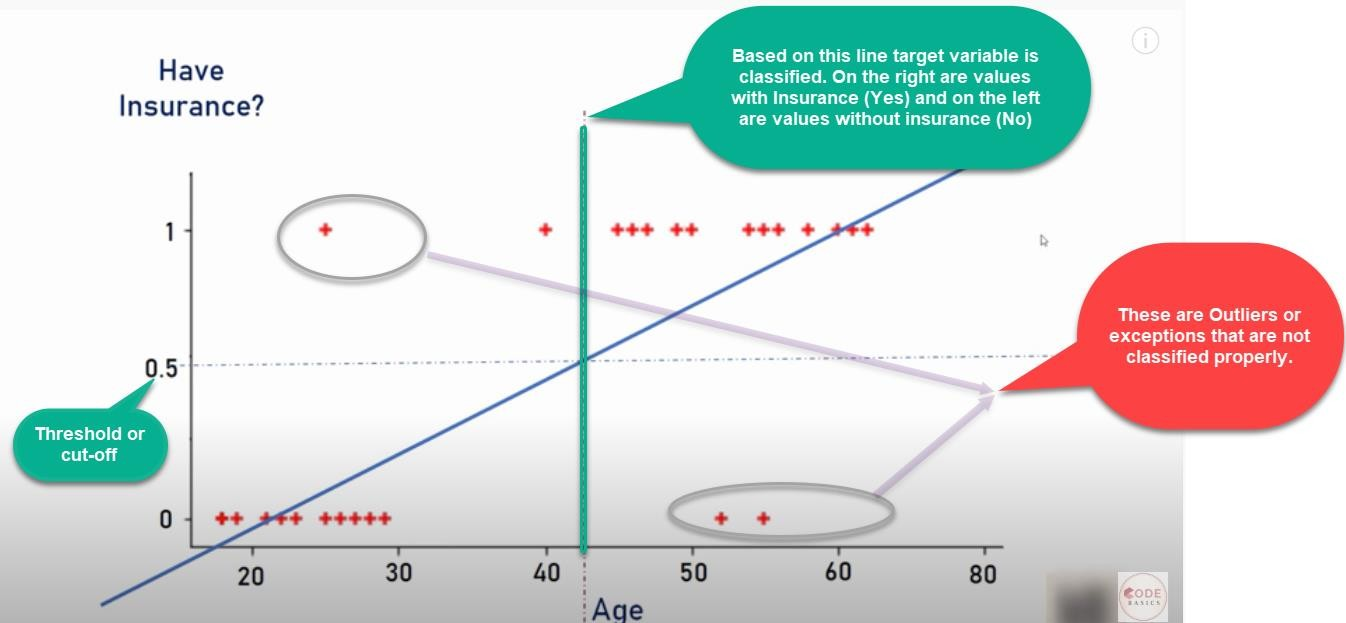
Ahora, imagina que hay un valor atípico hacia la derecha:

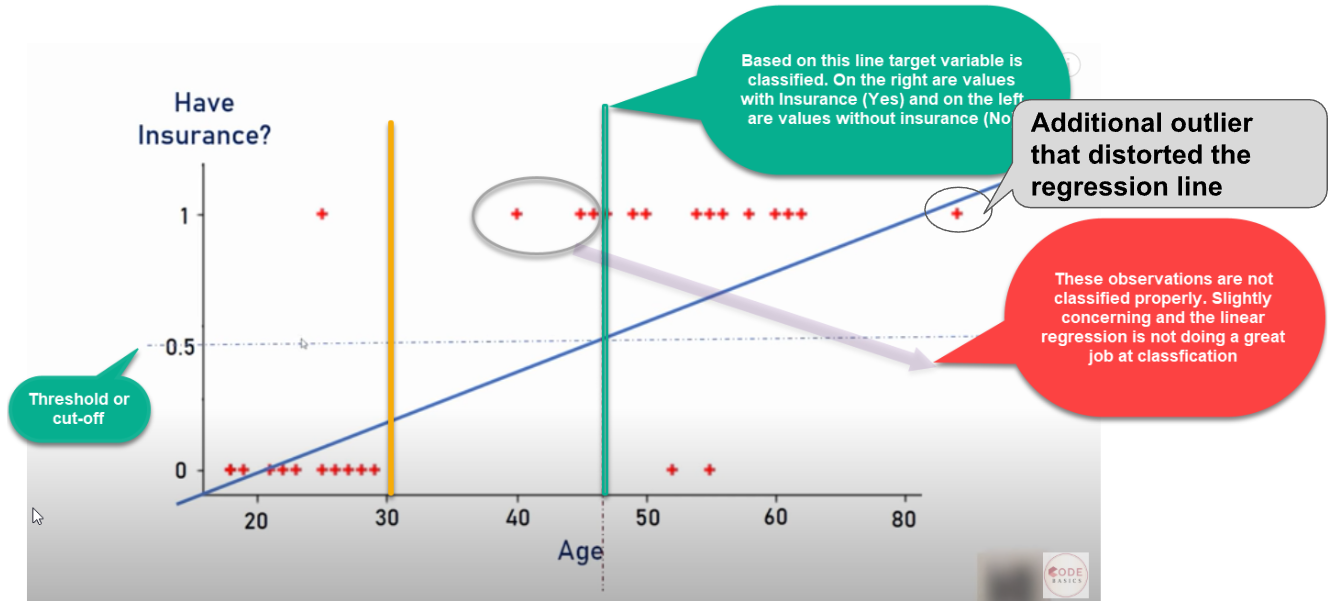
• Como podemos ver, un valor atípico en los datos distorsionará toda la línea de regresión lineal.
• Claramente, la línea no puede diferenciar las clases con el ajuste de línea lineal
• La línea debería haber estado en la línea amarilla vertical, que puede dividir las clases positivas y negativas, es decir, sí o no para el seguro

¡Feliz Juan! (Científico de datos)

• Bueno, la vida sería mucho más simple si tuviéramos un algoritmo que encajaría en los puntos como a continuación, ¿verdad? ¡Es un ajuste mucho mejor en comparación con la línea de regresión!

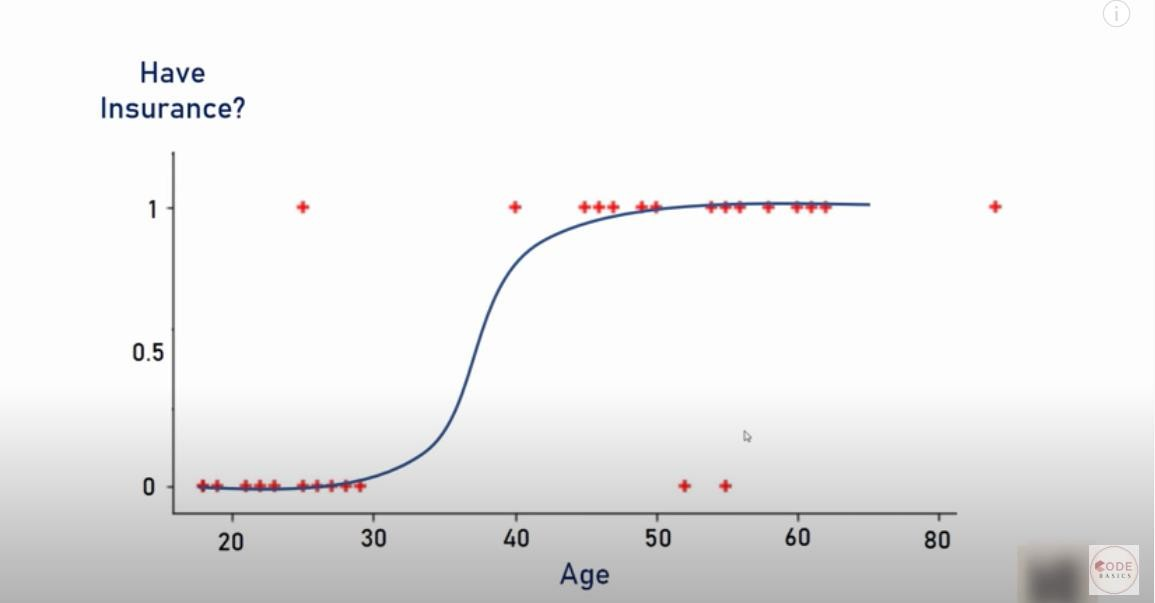
Solución

• Solución: transformar la regresión lineal en una curva de regresión logística
• La regresión logística es una función sigmoidea
• Ahora, ¿qué hace esta función sigmoidea?
  • La función sigmoidea toma cualquier valor real y da una probabilidad de salida entre 0 y 1

¿Qué hacemos en la Regresión Logística?

Usaremos la salida de valor real de un modelo de regresión lineal entre 0 y 1 y clasificaremos un nuevo ejemplo basado en un valor de umbral. La función utilizada para realizar este mapeo es la función sigmoidea.

La función sigmoidea está representada por la fórmula:

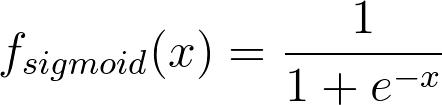
No hay necesidad de profundizar en cómo obtuvimos esta fórmula en este momento.

Función Sigmoidea (Función Logística/Logit)

• Tome la función de regresión lineal y colóquela en la función sigmoidea
• La función sigmoidea genera probabilidad entre 0 y 1

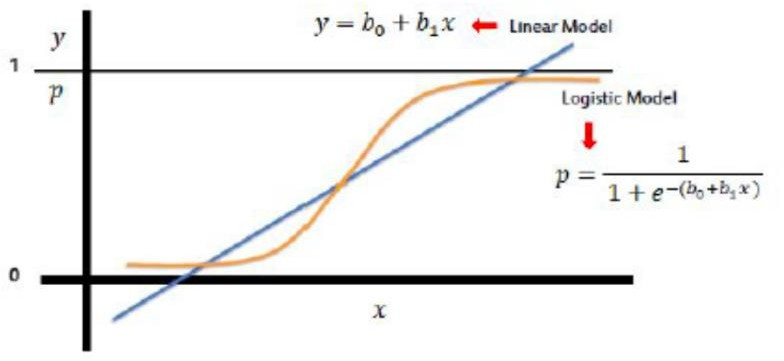
• La función sigmoidea genera probabilidad entre 0 y 1 (eje y)
• El umbral de probabilidad predeterminado se establece en 0,5 normalmente
  • Clase 0 – Por debajo de 0.5
  • Clase 1 – Por encima de 0,5

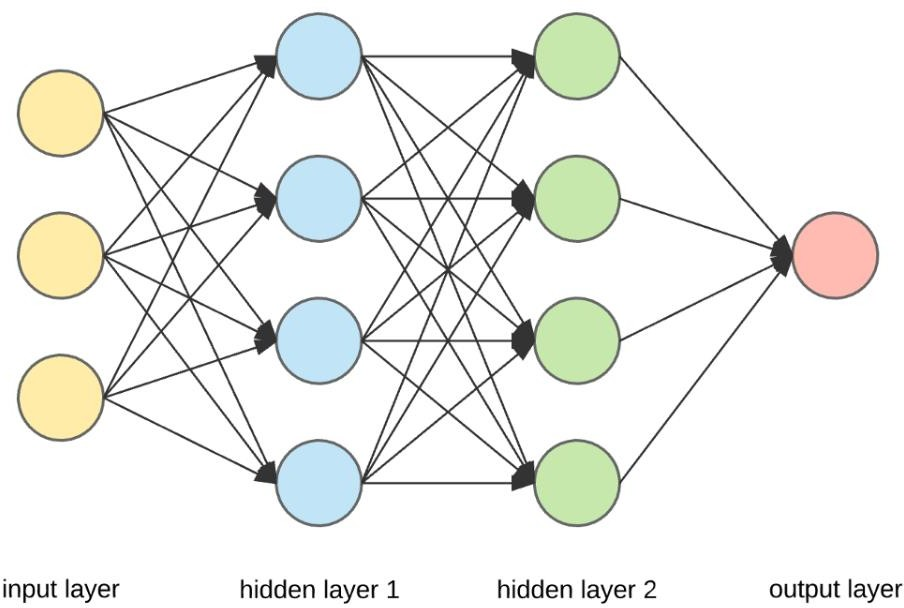
Funciones de activación

Así es como se ve una red neuronal. Vamos a sumergirnos un poco en qué sucede exactamente dentro de cada neurona.

Neurona artificial: un resumen rápido

Las neuronas artificiales son los componentes básicos de una red neuronal. Puede considerarse una unidad computacional que toma algunas entradas, aplica alguna transformación a la entrada y activa la salida. A continuación se muestran los pasos típicos para el cálculo dentro de la neurona.

1. Una neurona artificial toma las entradas y sus respectivas pesos
2. Luego aplica productos escalares entre los valores de entrada y sus pesos y los suma.
3. Finalmente, aplica la función de activación en la suma anterior y dispara la salida

Esto se puede escribir de una manera cruda de la siguiente manera:

Salida = Activación (Suma (Entradas * Pesos + Sesgo))

Referencia: machinelearningknowledge.ai

Dentro de una neurona

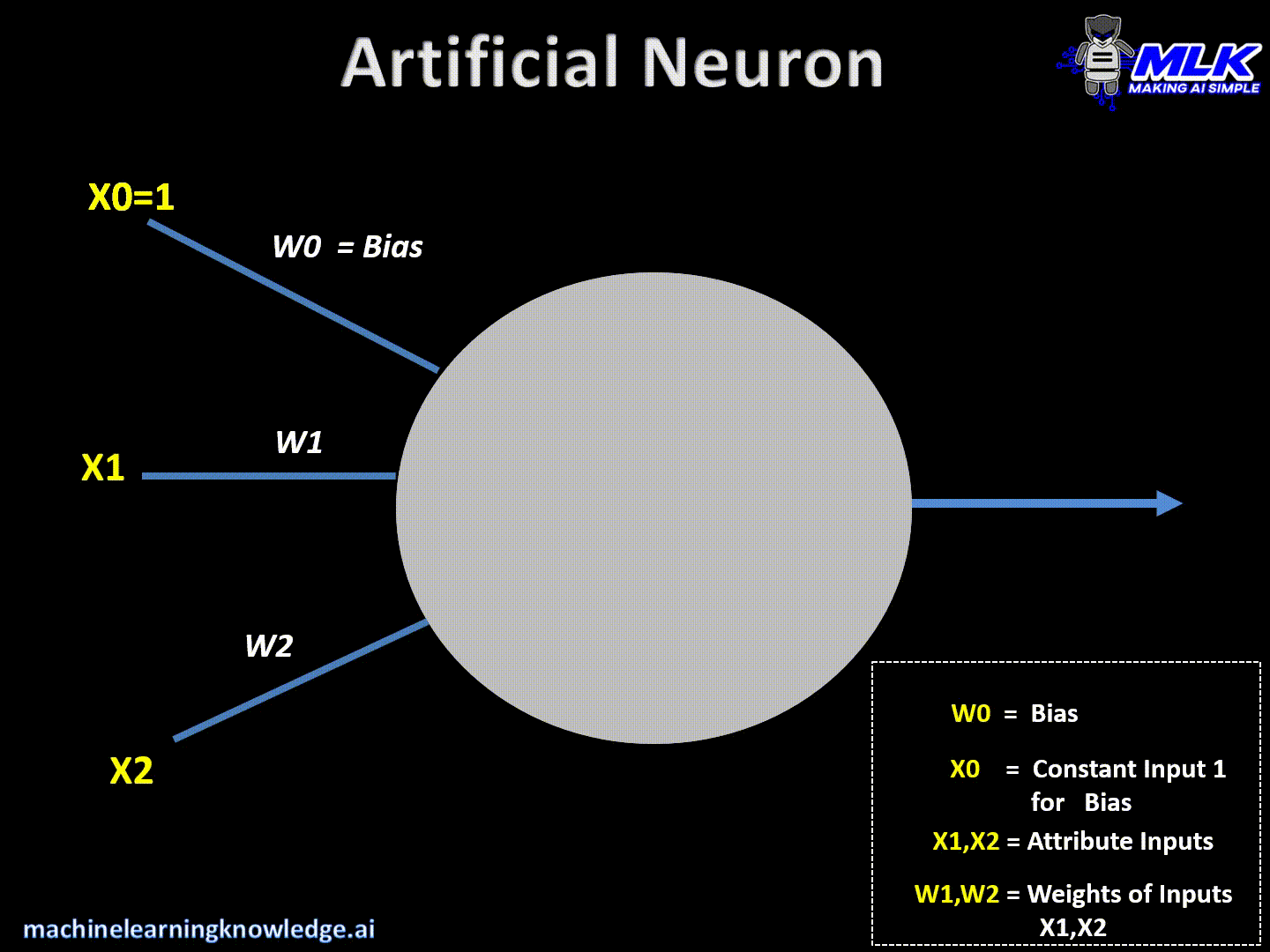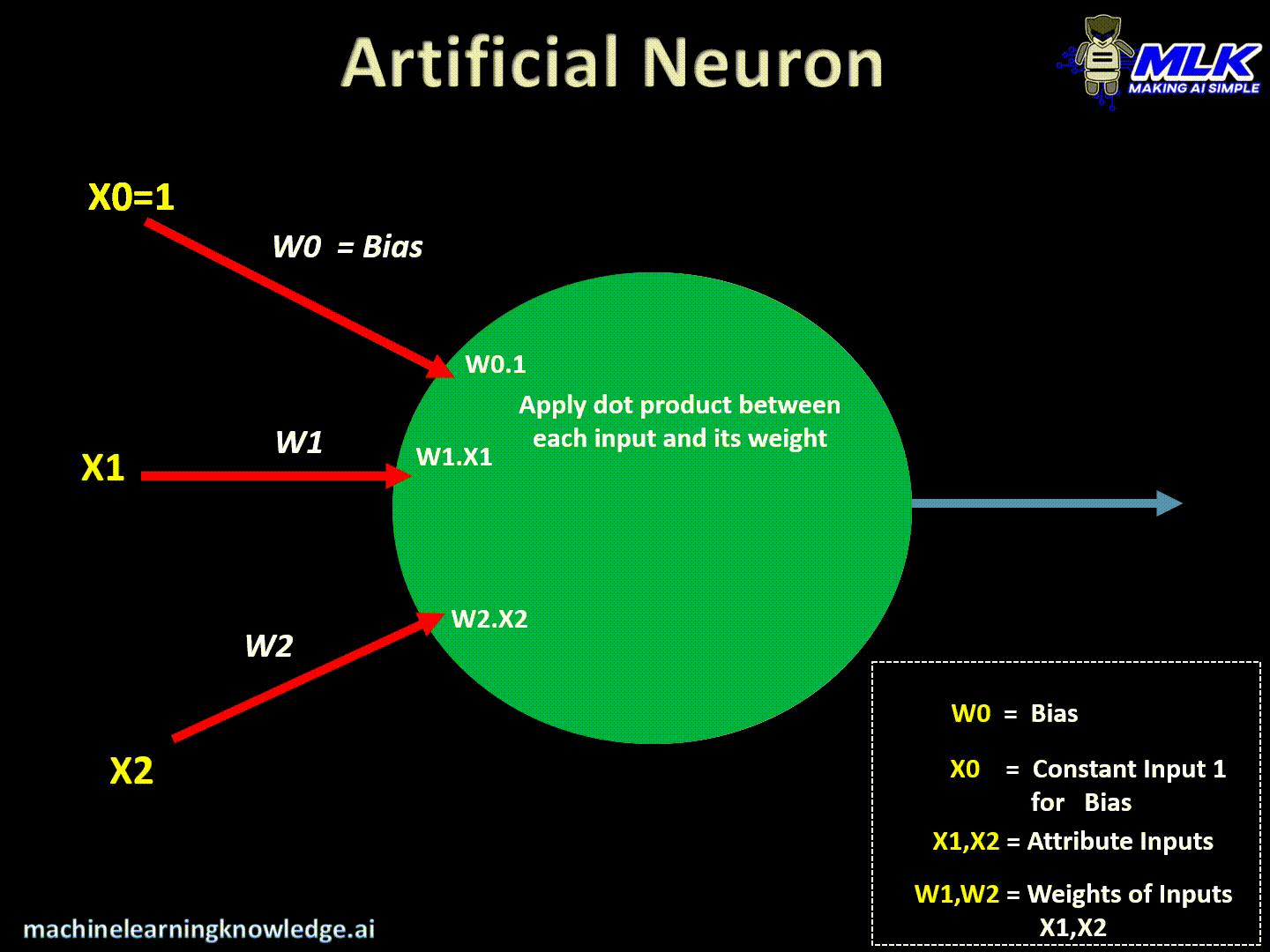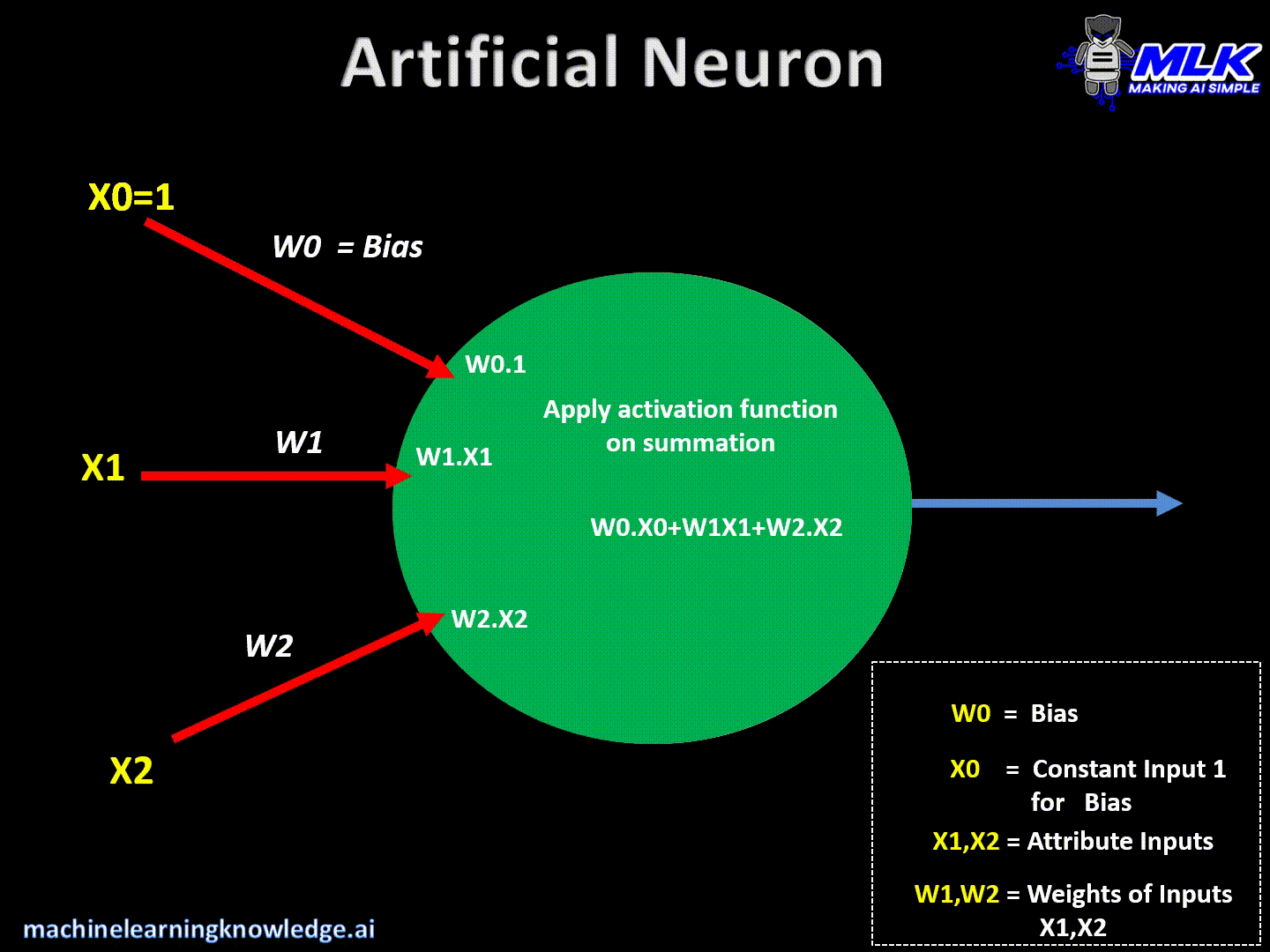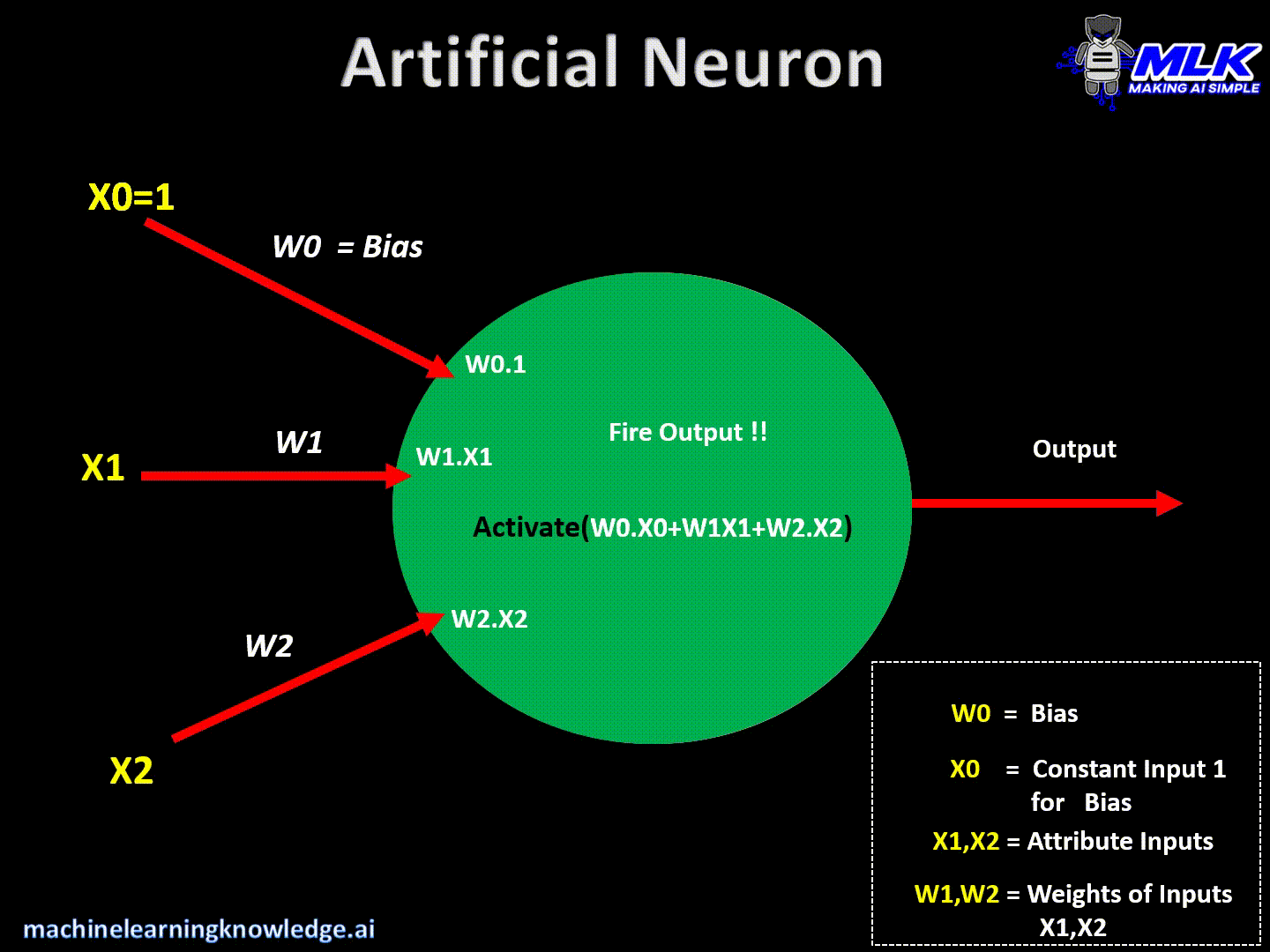
• Una neurona recibe información de las neuronas de la capa anterior (X0,X1,X2)
• Luego multiplica cada entrada con algún peso (W0, W1, W2) y los suma
• Finalmente, aplica alguna función de activación y envía/dispara una salida.

Funciones de activación

Las funciones de activación son una parte esencial de una red neuronal artificial.

Deciden si una neurona debe activarse (dispararse) o no en función de si la entrada de cada neurona es relevante para la predicción del modelo.

El propósito de la función de activación es introducir no linealidad en la salida de una neurona.

Básicamente, ayuda a crear un límite como este:

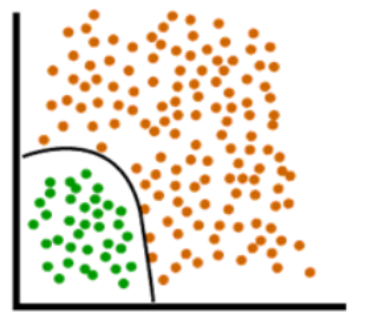
En lugar de los límites lineales (líneas rectas) que no pueden dividir los datos en dos clases:

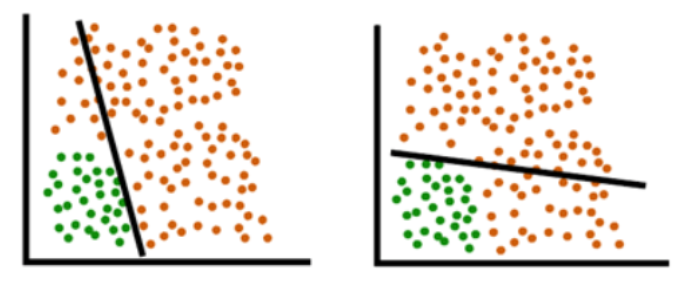
Tipos de funciones de activación

• Función sigmoidea
• ReLu
• bronceado
• ReLU con fugas
• Función Softmax y más...

Funciones de activación - ReLU

Similar a Sigmoid, tenemos muchas otras funciones de activación.

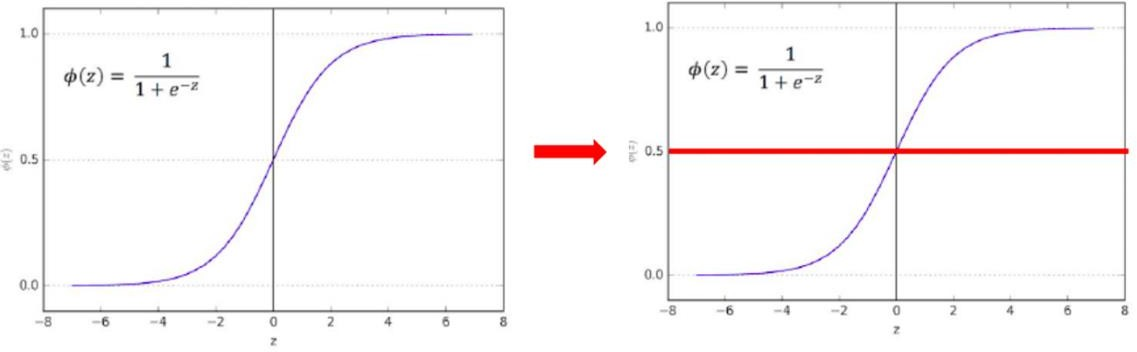
Echemos un vistazo a ReLU (Unidad lineal rectificada), por ejemplo:

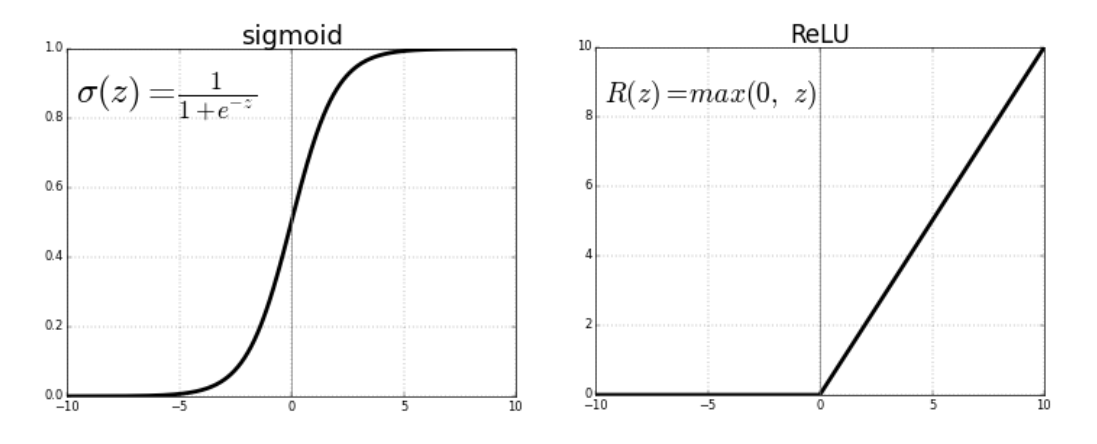
Mira el eje y de ambos gráficos. Así como Sigmoid tenía un rango de 0 a 1, ReLU tiene un rango de 0 a infinito.

Funciones de activación - tanh

Tanh / Hyperbolic Tangent es otra función de activación popular.

Comparte algunas cosas en común con la función de activación sigmoidea. Ambos se ven muy similares. Pero mientras una función sigmoidea tiene un rango de 0 y 1, Tanh tiene un rango de -1 y 1.

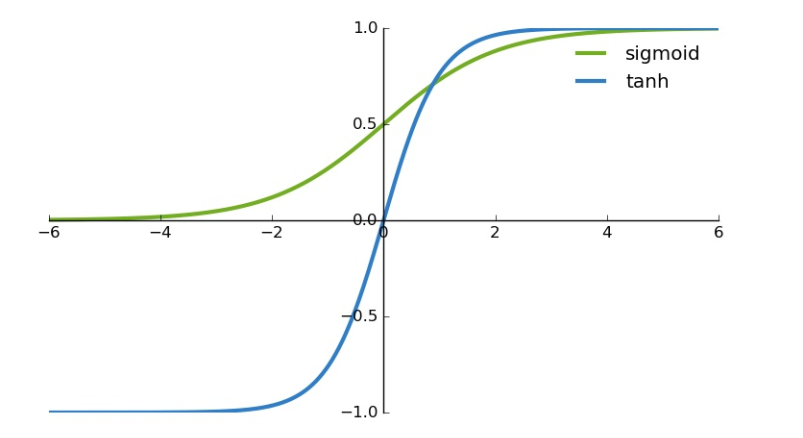
Hay algunas funciones de activación más sobre las que leeremos más adelante.

Reglas generales

Al elegir una función de activación, puede tener en cuenta las siguientes pautas:

• Sigmoid se usa comúnmente en la capa de salida. Esto se debe a que ayuda a dar una probabilidad (valor entre 0 y 1) que es útil en la clasificación binaria.
• En lugares que no sean la capa de salida, tanH suele funcionar mejor que Sigmoid.
• Para las capas ocultas, si no está seguro de qué función de activación usar, use ReLU como su opción predeterminada.

Nota: Si bien estas pautas son útiles, la elección de una función de activación también depende de prueba y error. Debe probar algunas funciones de activación y ver cuál funciona mejor.

Obtenga más información sobre las funciones de activación

• Guía animada de funciones de activación en redes neuronales
• El artículo anterior explica la necesidad de funciones de activación, los diferentes tipos de activaciones, así como las ventajas y desventajas de cada uno.
• Recomendamos echarle un vistazo para tener una idea a través de los diversos gifs presentes.
• No hay necesidad de sumergirse en las matemáticas o preocuparse por los términos técnicos utilizados allí; llegaremos a ello en unos días. El proceso de aprendizaje es lento pero seguramente constante :)

Capas

Las neuronas en una red neuronal se dividen en capas.

Si bien los conocemos por los nombres Input, Hidden y Output hasta ahora, Tensorflow no tiene esos nombres. Quiere que el usuario especifique el tipo de esa capa en particular.

Para utilizar los diferentes tipos de capas que tenemos disponibles, Tensorflow proporciona un submódulo llamado capas que podemos importar de la siguiente manera:

Capa densa

• Una capa densa es solo una capa regular de neuronas en una red neuronal.
• Es la capa más común y de uso frecuente.
• Mira la capa intermedia en la imagen anterior. Cada neurona recibe información de todas las neuronas de la capa anterior y, por lo tanto, se denomina densamente conectada o densa.
• Cada salida de una capa densa se calcula usando cada entrada a la capa.
• Densa es un tipo particular de capa, pero veremos muchos otros tipos a medida que continuamos nuestro viaje de aprendizaje profundo.

Creando modelos con Capas

API de modelo secuencial

Hay dos formas de crear un modelo utilizando la API de capas:

1. Un modelo secuencial El tipo de modelo más común es el modelo secuencial, una pila lineal de capas. En resumen, le permite construir un modelo capa por capa. Cada capa tiene pesos que corresponden a la capa que le sigue.
2. Un modelo funcional A diferencia de la pila de capas en la API secuencial, la API funcional es una forma de crear gráficos de capas.

Como principiante, el modelo secuencial es la forma recomendada de empezar.

CONSEJO: Aprender haciendo

NO necesita memorizar el código dado en el cuaderno a continuación. Pero debe comprender lo que hace cada línea de código y debe poder replicarlo si es necesario para resolver otros problemas. Hemos proporcionado explicaciones tanto como sea posible; Si aún no obtiene ciertas cosas, ¡no dude en preguntar en el [Discord Server] (https://discord.gg/E2XfSEYm2W)!

¡Practiquemos la construcción de modelos secuenciales y funcionales!

Cuaderno para la creación de modelos

• Descargar
• Extraiga el archivo zip
• Abrir en Jupyter Notebook o cargar en Google Colab

Funciones de error y optimizadores

Funciones de error/pérdida

En la mayoría de las redes de aprendizaje, el error se calcula como la diferencia entre el resultado real y el previsto.

La función que se utiliza para calcular este error se conoce como función de pérdida.

Diferentes funciones de pérdida darán diferentes errores para la misma predicción y, por lo tanto, tendrán un efecto considerable en el rendimiento del modelo.

Para los problemas de clasificación binaria, la función de pérdida que se suele utilizar se conoce como pérdida de entropía cruzada binaria. No necesitamos entrar en las profundidades de esta pérdida en este momento. Esto se tratará en sesiones posteriores.

Función de optimización

El error es una función de los parámetros internos del modelo, es decir, los pesos y el sesgo. Por ejemplo, m y c en una ecuación de línea recta.

Para predicciones precisas, es necesario minimizar el error calculado.

En una red neuronal, esto se hace mediante retropropagación. El error actual generalmente se propaga hacia atrás a una capa anterior, que se usa para modificar los pesos y el sesgo para minimizar el error.

Los pesos se modifican mediante una función denominada Función de Optimización. Las funciones de optimización suelen calcular el gradiente.

Hay varios optimizadores disponibles, como Adam, RMSProp, SGD, etc. No es necesario entrar en la teoría detrás de estos optimizadores, ya que esto también se tratará más adelante.

Para nuestro problema, usaremos RMSProp como optimizador.

Por lo tanto, los componentes de un modelo de red neuronal, es decir, la función de activación, la función de pérdida y el algoritmo de optimización, juegan un papel muy importante en el entrenamiento eficiente y efectivo de un modelo para producir resultados precisos.

Diferentes tareas requieren un conjunto diferente de tales funciones para dar los resultados más óptimos.

Enlace de descarga de diapositivas

Puede descargar las diapositivas de este módulo aquí