Earn 20 XP

Learning Objectives

  • Difference between Classification and Regression
  • Regression Algorithms & Model Evaluation Metrics
  • Which evaluation metrics to use when?

Disclaimer

  • We haven't taught all the algorithms as the Bootcamp was for five weeks, and we wanted learners to grasp the concepts and not overwhelm them with all the available concepts. Once you know how to handle data and build models, you can easily create different kinds of models.
  • Through this module, we'll be providing material around some of the popular algorithms. In addition, we will be sharing some more resources soon.

Classification vs Regression

image.png

image.png

  • To decide whether to use a regression or classification model, the first question you should ask yourself is:
  • Does your target variable have a continuous value, or is it discrete (binary or multi-class)?

Regression

  • If your answer is continuous values, you're dealing with regression.
  • This means that if you're trying to predict quantities like height, income, price, or scores, you should use a model that will output a continuous number.
  • So, if your objective is to determine tomorrow's temperature (or, say, stock price tomorrow), you should use a regression model.

Classification

  • Let's come to the second case where you can see that the target variable is divided into classes. You'll be using Classification here.
  • When the number of classes is 2, it is known as Binary Classification.
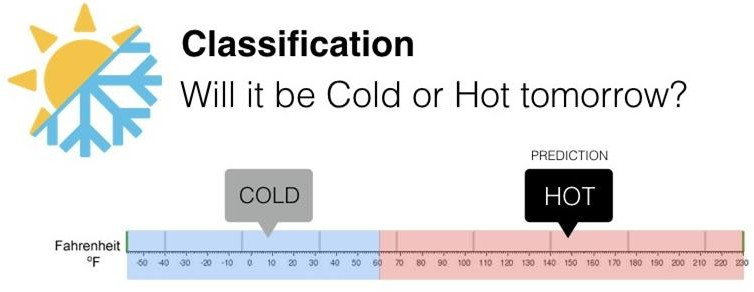
  • Eg. Will it be hot or cold tomorrow is a binary classification problem with two classes: Hot and Cold.
  • When it is more than 2, it is known as Multi Class Classification.
  • Eg. Classifying movies as Good, Average, or Bad according to reviews.

Classification vs Regression

image.png

Understanding your target variable's characteristics is essential before you begin running models and forming predictions.

Types of Regression Algorithms

  1. Linear Regression
  2. Decision Trees (DecisionTreeRegressor)
  3. Random Forest (RandomForestRegressor)
  4. Other Algorithms
    1. Polynomial Regression
    2. Lasso, Ridge, and Elastic Net Regression
    3. Support Vector Regressor
    4. And many more.

Linear Regression

Decision Trees for Regression - Regression Trees

Decision Trees

  • Regression tree analysis is used when the predicted outcome can be considered a real number (e.g. the price of a house, or a patient's length of stay in a hospital).
  • Note: Something that we didn't address earlier, Decision Trees are also called Classification And Regression Trees (CART).
  • Reason: They can be used in both regression and classification contexts. For this reason, they are sometimes called Classification And Regression Trees (CART).
  • Module on Decision Trees: https://docs.google.com/presentation/d/1BCwLdFQqFLHR2-7APyoWh5u1b6Jo3wq17nj-8s2H\_mg/edit#slide%3Did.p1

Resources on Decision Tree Regressor

Random Forest for regression - Regression Forest

  • Random forest builds multiple decision trees and merges them to get a more accurate and stable prediction.
  • Regression Forests (or Random forest Regressors) are an ensemble (combination) of different regression trees (decision trees for regression). Each leaf contains a distribution for the continuous output variable/s.

image.png

Other Regression Algorithms

  • POLYNOMIAL REGRESSION:

Polynomial regression is a form of linear regression in which the relationship between the independent variable X and dependent variable y is not linear (cannot be represented by a straight line).

image.png

Which of the following do you think is a better-fitted line for the green data points?

The second one. The only difference is that instead of using the equation of a straight line, we are using a different equation of higher order polynomial.

Learn more about Polynomial Regression: https://towardsdatascience.com/polynomial-regression-bbe8b9d97491

  • LASSO, RIDGE, AND ELASTIC NET REGRESSION:

There are extensions of the linear regression model training called regularization methods. They aim to minimize the error while keeping the complexity of the model low.

Two popular examples of regularization procedures for linear regression are:

  1. Lasso Regression (called L1 regularization).
  2. Ridge Regression: (called L2 regularization).

These methods are effective when there is collinearity in your input variables, and there's a chance of overfitting the training data.

There is another commonly used model of regression called Elastic Net. It incorporates penalties from both L1 and L2 regularization.

You can read more about Lasso, Ridge, and Elastic Net Regression here:

https://hackernoon.com/an-introduction-to-ridge-lasso-and-elastic-net-regression-cca60b4b934f

  • SUPPORT VECTOR REGRESSOR (SVR)

Support Vector Machines (SVMs) are well known in classification problems. However, the use of SVMs in regression is not as well documented. These types of models are known as Support Vector Regression (SVR).

SVR gives us the flexibility to define how much error is acceptable in our model and will find an appropriate line to fit the data.

SVR Tutorial:

https://www.analyticsvidhya.com/blog/2020/03/support-vector-regression-tutorial-for-machine-learning/

MUST READ - Regression Algorithms and their applications:

Regression Model Evaluation

  1. Cost function
  2. What is the predicted and expected/actual value?
  3. Evaluation Metrics
    1. RMSE
    2. MAE
    3. MSE

Cost Function

What?

  • Now that we built a model, we need to measure its performance, right? and understand if it works well or not. The cost function measures the performance of a Machine Learning model for given data. It quantifies the error between predicted and expected values and presents it as a single real number.
  • Depending on the problem, Cost Function can be formed in many different ways. The purpose of this function is to be either:
  • Minimized - the returned value is usually called cost, loss, or error. The goal is to find the values of model parameters for which Cost Function returns as small a number as possible.
  • Maximized - the value it yields is named a reward. The goal is to find values of model parameters for which returned number is as large as possible.

What is the predicted and expected value?

  • Predicted value: As the name says is the predicted value of your machine learning model.
  • Expected/Actual value: Is the true value(or the label present in your data)
  • Often, machine learning models are not 100% accurate or perfect and tend to deviate from the actual or expected value.
  • Explaining with an example: If we are predicting a person's age based on a few input variables or features.
  • Our machine learning model predicted the age as 28 years
  • However, the actual age of the person is 29 years.
  • Here 28 years is the predicted value and 29 years is the expected or actual value. As data scientists, we try to minimize errors while building models.

Cost Function

image.png

  • The difference between the actual value and the model's predicted value is called residual.

Cost Function Types/Evaluation Metrics

  • There are three primary metrics used to evaluate linear models (to find how well a model is performing):
    • Mean Squared Error:
    • Root Mean Squared Error
    • Mean Absolute Error

Mean Squared Error (MSE)

  • MSE is simply the average of the squared difference between the true target value and the value predicted by the regression model.
  • As it squares the differences, it penalizes (gives some penalty or weight for deviating from the objective) even a small error which leads to over-estimation of how bad the model is.

image.png

Root Mean Squared Error (RMSE)

  • It is just the square root of the mean square error.
  • It is preferred in some cases because the errors are first squared before averaging, which poses a high penalty on large errors. This implies that RMSE is useful when large errors are undesired.

image.png

Mean Absolute Error(MAE)

  • MAE is the absolute difference between the target value and the value predicted by the model.
  • MAE does not penalize the errors as effectively as MSE, making it unsuitable for use-cases where you want to pay more attention to the outliers.

image.png

R Squared ( Coefficient of determination)

  • R-squared is a goodness-of-fit measure for linear regression models.
  • It represents the coefficient of how well the values fit compared to the original values. The values from 0 to 1 are interpreted as percentages.
  • The higher the value is, the better the model is.
  • Going by the name, you might think R2 cannot be negative. However, it can. A Negative R2 means you are doing worse than the mean value.

Which metrics to use when?

This is an important question, and we get used to learning these measures over time. Sharing some resources with you all so that it helps you understand what metrics to use in the context of solving a regression problem.