Neural Networks for Regression | AI Planet (formerly DPhi)

This is an optional video. Go through it if you don’t know what a slope of a line is.

In algebra, a linear equation (equation of a straight line) typically takes the form y = mx + b, where m and b are constants, x is the independent variable, and y is the dependent variable.
Basically, the value of y is calculated using x, whereas x has no dependence on the value of y.
y = how far up
x = how far along
m = Slope or Gradient (how steep the line is)
b = value of y when x=0

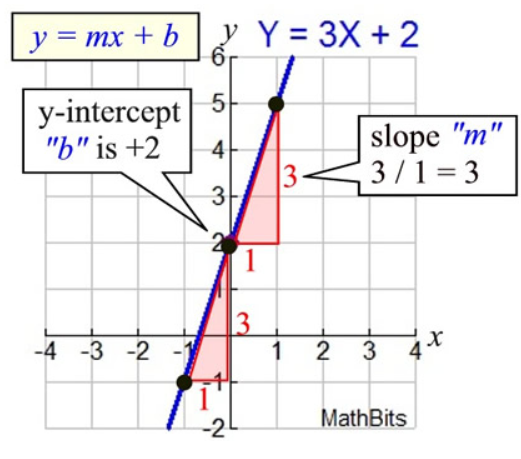
How do you find "m" and "b"?
- b is easy: see where the line crosses the Y axis.
- m (the Slope) needs some calculation:

Suppose you are thinking of selling your home. And, various houses around you with different sizes (area in sq.ft) around you have sold for different prices as listed below:

And considering, your home is 3000 square feet. How much should you sell it for?
When you look at the existing price patterns (data) and predict a price for your home that is an example of linear regression.
Here's an easy way to do it. Plotting the 3 data points (information about previous homes) we have so far:

Now you can eyeball it and roughly draw a line that gets pretty close to all of these points. Then look at the price shown by the line, where the square footage is 3000:

Boom! Your home should sell for $260,000.
That's all! (Well kinda) You plot your data, make a rough line, and use the line to make predictions. You just need to make sure your line fits the data well (but not too well :)

But of course we don't want to roughly make a line, we want to compute the exact line that best "fits" our data. That’s where

Linear regression is a linear model i.e. a model that assumes a linear relationship (straight-line relationship) between the input variables (x) and the single output variable (y).
When there is a single input variable (x), the method is referred to as simple linear regression or just linear regression. Eg: Salary dataset given here. There is only one target variable and one input variable where we are predicting the salary of individual using their years of experience.
When there are multiple input variables, it is often referred to as multiple linear regression. Eg: Smart Metropolitan areas data set, we have multiple input variables.

This above drawn line is way oﬀ. For example, according to the line, a 1000 sq foot house should sell for $310,000, whereas we know it actually sold for $200,000.

In the video instead of house size and it’s price, the tutor has used height and weight of people. There is nothing to worry. Just understand the residual concept.

The residual (absolute diﬀerence between the actual and the predicted value) in this case are: $5000, $15000 and $5000.
This line is an average of $8,333 dollars oﬀ (adding all the distances and dividing by 3).
This $8,333 is called the cost of using this line.

The cost is how far oﬀ the learned line is from the real data. The best line is the one that is the least oﬀ from the real data.
To find out what line is the best line (to find the values of coeﬃcients), we need to define and use a cost function.
In ML, cost functions are used to estimate how badly models are performing.
Put simply, a cost function is a measure of how wrong the model is in terms of its ability to estimate the relationship between X and y.

There is also something called as Cost function that is associated with the analysis, it is slightly mathematical, we will be learning more about it soon!
Meanwhile, let’s run a simple linear regression model using tf.keras. The link to notebook is given towards the end.

A technique to minimize cost by computing the gradients of cost with respect to the model's parameters, conditioned on training data. Informally, gradient descent iteratively adjusts parameters, gradually finding the best combination of weights and bias to minimize cost.

What is bias?

An intercept or offset from an origin. Bias (also known as the bias term) is referred to as b or w0 in machine learning models. For example, bias is the b in the following formula: y = mx + b.

Hyperparameters are those parameters of the model whose values affects the model’s performance.
We change the values of these hyperparameters during successive runs of training a model.
Here you will learn three important hyper parameters:
- Learning Rate
- Epoch
- Batch Size

A scalar used to train a model via gradient descent. During each iteration, the gradient descent algorithm multiplies the learning rate by the gradient.
The resulting product is called the gradient step. Learning Rate is a key hyperparameter.
Don’t worry if you don’t understand it, you will understand this when you will be introduced to Gradient Descent.
For the time being, just consider it as a hyperparameter of the deep learning model whose values effects the performance of the model

This is nothing but the number of loops that you want through the training dataset.

A model has a life-cycle, and this very simple knowledge provides the backbone for both modeling a dataset and understanding the tf.keras API.
The five steps in the life-cycle are as follows:
- Define the model.
- Compile the model.
- Fit the model.
- Make predictions on the test data.
- Evaluate the model.
The above 5 steps are explained in the notebook with practical implementation.